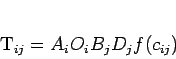suivant: Estimation de la fonction
monter: Méthode d'estimation des matrices
précédent: Méthode d'estimation des matrices
Table des matières
C'est un moyen de déterminer les éléments  de la matrice de déplacements que l'on souhaite reconstituer.
L'idée est de reproduire le phénomène physique de l'attraction de Newton. Une des formulations les plus aboutie
est littéralement donnée par:
de la matrice de déplacements que l'on souhaite reconstituer.
L'idée est de reproduire le phénomène physique de l'attraction de Newton. Une des formulations les plus aboutie
est littéralement donnée par:
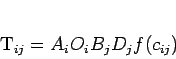 |
(2.1) |
On fait ainsi intervenir :
- Les volumes d'entrée et sortie des zones origines et destinations (déterminés lors de la première
étape),
- des "coefficients balances"
 et
et 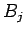 ,
,
- une fonction
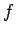 à déterminer.
à déterminer.
Les coefficients balance sont définis par :
Ils sont déterminés par itérations successives, en prenant tous les 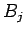 égaux à 1 comme conditions
initiales par exemple et jusqu'a convergence du processus.
Ceux-ci servent à se caler sur les marges. Effectivement dans l'équation (2.1), en sommant les
égaux à 1 comme conditions
initiales par exemple et jusqu'a convergence du processus.
Ceux-ci servent à se caler sur les marges. Effectivement dans l'équation (2.1), en sommant les  sur j,
on retrouve
sur j,
on retrouve  en ramplaçant les
en ramplaçant les  et
et 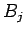 par leurs valeurs respectives.
par leurs valeurs respectives.
La fonction 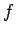 dite fonction d'impédance met en évidence la relation au coût de déplacement, intrinsèque à
l'éloignement respectif des zones. Les formes les plus utilisées pour cette fonction sont :
dite fonction d'impédance met en évidence la relation au coût de déplacement, intrinsèque à
l'éloignement respectif des zones. Les formes les plus utilisées pour cette fonction sont :
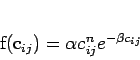 |
(2.2) |
La fonction à interpoler est obtenue à partir d'une analyse croisée de la table des déplacements.
Ces derniers sont comptabilisés par tranches de 5 minutes par exemple. La représentation graphique
du résultat est donnée par la figure (2.1).
Figure:
Distribution observée du coût des déplacements en zone urbaine
|
|
Etrangement, peut-être par facilité, la plupart des modèles mis en place lors d'études
antérieures utilisent l'expression exponentielle seule. Pourtant il semble que la
formule la plus élaborée soit celle donnée par l'equation (2.2).
Une telle fonction combinant un terme polynomial et un terme
exponentiel rend compte de la dépression initiale contrairement
à une exponentielle pure qui est strictement décroissante.




suivant: Estimation de la fonction
monter: Méthode d'estimation des matrices
précédent: Méthode d'estimation des matrices
Table des matières
2003-06-21