



suivant: La méthode de dichotomie
monter: Etude numérique
précédent: Etude numérique
Table des matières
La méthode s'inpspire du celle du gradient conjugué.
Algorithme :
- choisir
 .
.
calculer
 , et poser
, et poser  .
.
- Etape k.
 où
où  minimise
minimise
 .
.
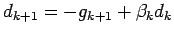
avec
 et
et
 .
.
Une de nos difficultés a porté sur le calcul de  :
:
avec :
On examine les six triangles voisins du point  , la dérivée étant nulle ailleurs.
, la dérivée étant nulle ailleurs.
Figure:
Triangles adjacents à 
|
|
donc on a :
où
avec
d'où
La formule est valable pour les six triangles voisins du point  .
.
Au total, on obtient
 .
.




suivant: La méthode de dichotomie
monter: Etude numérique
précédent: Etude numérique
Table des matières
2003-06-22




