



suivant: Résolution numérique
monter: Le modèle de choix
précédent: Le modèle Logit
Table des matières
Une fois faite la spécification des variables, il s'agit d'estimer la valeur des paramètres des fonctions d'utilité.
La méthode employée est celle du maximum de vraisemblance. Nous allons chercher les  tels
que la situation observée (échantillon extrait de l'enquête ménage) ait la plus grande probabilité de
se produire, connaissant la loi du modèle (ici le Logit).
tels
que la situation observée (échantillon extrait de l'enquête ménage) ait la plus grande probabilité de
se produire, connaissant la loi du modèle (ici le Logit).
La vraisemblance de l'échantillon s'écrit :
 |
(2.5) |
avec :
et on cherche :
Il s'agit d'un problème non linéaire sans contraintes.
Soit
 , la log-vraisemblance. On a alors :
, la log-vraisemblance. On a alors :
avec :

d'où:
Au total:
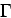 |
(2.6) |
Nous cherchons donc à maximiser la fonction  telle qu'elle est formulée dans l'équation (2.6) en fonction des paramètres
telle qu'elle est formulée dans l'équation (2.6) en fonction des paramètres  .
.
Théorème 2
Dans le cas d'un Logit multinomial, la log-vraisemblance est concave.
Preuve Voir [5],page 16.
Cette propriété est fondamentale, elle garantit l'unicité de la solution au problème.
Nous allons donc chercher à résoudre
 , condition nécessaire à l'optimalité de la solution.
, condition nécessaire à l'optimalité de la solution.
Déteminons les dérivées partielles :
d'où :
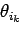 |
(2.7) |
Remarque :
 est un paramètre qui peut correspondre à :
est un paramètre qui peut correspondre à :
- une variable continue,
- une variable à modalités,
- la constante de l'utilité TC ou de l'utilité VP.
La formule 2.7 est valable dans le premier cas.
Dans le deuxième la formule est la même, seulement, 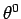 vaut 1 si l'individu n a pour caractéristique la modalité qui correspond
à
vaut 1 si l'individu n a pour caractéristique la modalité qui correspond
à  , 0 sinon.
, 0 sinon.
Dans le dernier cas, 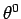 vaut 1.
vaut 1.




suivant: Résolution numérique
monter: Le modèle de choix
précédent: Le modèle Logit
Table des matières
2003-06-21


 , la log-vraisemblance. On a alors :
, la log-vraisemblance. On a alors :
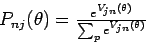

![\begin{displaymath}
\Gamma (\theta )=\sum_n \sum_j \left[ g_{jn}.\ln\left( \frac{e^{V_{jn}(\theta)}}{\sum_p e^{V_{pn}(\theta)}}\right) \right]
\end{displaymath}](img58.png)
![\begin{displaymath}
\Rightarrow
\Gamma (\theta )=\sum_n \sum_j \left[ g_{jn}.V...
...-g_{jn}. \ln \left( \sum_p e^{V_{pn}(\theta)} \right) \right]
\end{displaymath}](img59.png)
![\begin{displaymath}
\Rightarrow
\Gamma (\theta )=\sum_n \sum_j \left( g_{jn}.V...
... g_{jn}. \ln \left( \sum_p e^{V_{pn}(\theta)} \right) \right]
\end{displaymath}](img60.png)

 , condition nécessaire à l'optimalité de la solution.
, condition nécessaire à l'optimalité de la solution.




est un paramètre qui peut correspondre à :
vaut 1 si l'individu n a pour caractéristique la modalité qui correspond à
, 0 sinon.
vaut 1.